New Distance-Biregular Graphs, Twin-Width of SRGs & a Covering Problem

April has been a very busy month for me for various reasons. One of them is that I had three preprints put on the arXiv:

• New Constructions of Distance-Biregular Graphs in joint work with Blas Fernández, Sabrina Lato, and Akihiro Munemasa. This I am extremely happy about as we give the first genuinely new constructions for distance-biregular graphs in over 30 years. (What I mean by “genuinely” I will explain below.) Plus some non-existence conditions.
• On the twin-width of near-regular graphs in joint work with Irene Heinrich, Simon Raßmann, and Lena Volk. Here we investigate the twin-width of some very regular graphs like strongly regular graphs.
• Small genus, small index critical points of the systole function in joint work with Ni An and Ingrid Irmer. This is about a covering problem in so-called Teichmüller spaces.

Let me discuss all of these here with a focus on the first of the three. In each case I try to focus on aspects which are not the focus of the respective preprints. I will keep the discussion more casual and refer to the papers for formalities.

1. Distance-Biregular Graphs (DBRGs)

The main theme, as far as I see, of distance-biregular graphs (DBRGs) is to give a bipartite version of distance-regular graphs. Distance-regular graphs are very relevant for other areas of mathematics, for instance they provide an algebraic framework for parts of coding theory or extremal graph theory. While the theory of DBRGs arose in the 1980s, I feel that with these motivations on mind, it is important to study. For instance, in many Ramsey and Turan problems in extremal graph theory, it seems to be clear that bipartite graphs coming from finite geometry are the object which one wants to study. The most prominent example is the determination (up to a log factor) of the asymptotic behavior of the Ramsey number $ {R(4, t)}$ by Mattheus and Verstraete, but there are other examples too. Distance-biregular graphs capture the most regular of such graphs, with generalized polygons being their most famous representative (also with applications in extremal graph theory). The list of feasible distance-biregular graph parameters seems to suggest there is a variety of interesting constructions to be found which use finite geometry.

Unlike strongly regular graphs, genuinely distance-biregular graphs are extremely rare which makes their construction very exciting. But what do I mean by genuine? Generalized polygons, Steiner triple systems, quasi-symmetric designs, the bipartite doubles of strongly regular graphs, and the bipartite doubles of distance-regular graphs all give rise to distance-biregular graphs. A reasonable study of DBRGs excluded all of these objects as they have their own communities. Note that there is also a nice hierarchy: If you have a distance-biregular graph, then the distance-$ {2}$-graph on each of the two halves is a distance-regular graph (even though sometimes the one half is trivial in some sense).

Before I start with the actual discussion, I want to digress a little and mention how this collaboration was quite cool in how it came together. From my point of view it was as follows: Sabrina Lato, who is currently based in Sweden, asked finite geometers in Europe about possible constructions. They (more specifically: Anurag Bishnoi) referred her to me. At the same time Blas Fernández and Akihiro Munemasa were discussing DBRGs. Then at the G2C2 conference in Shijiazhuang in August 2025, which I and Akihiro attended, we noticed this. Then, in September first Sabrina visited me for two weeks, then Akihiro. All thanks to the generous funding of my department and the startup grant by the city of Shenzhen.

2. New DBRGs

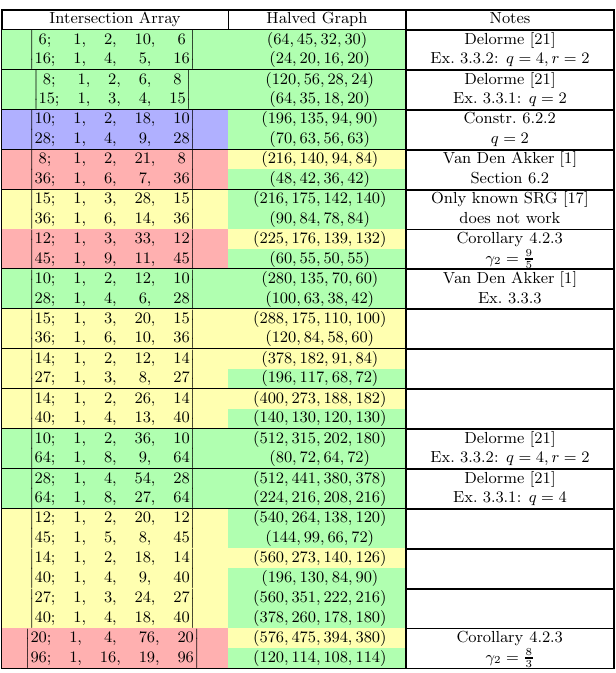
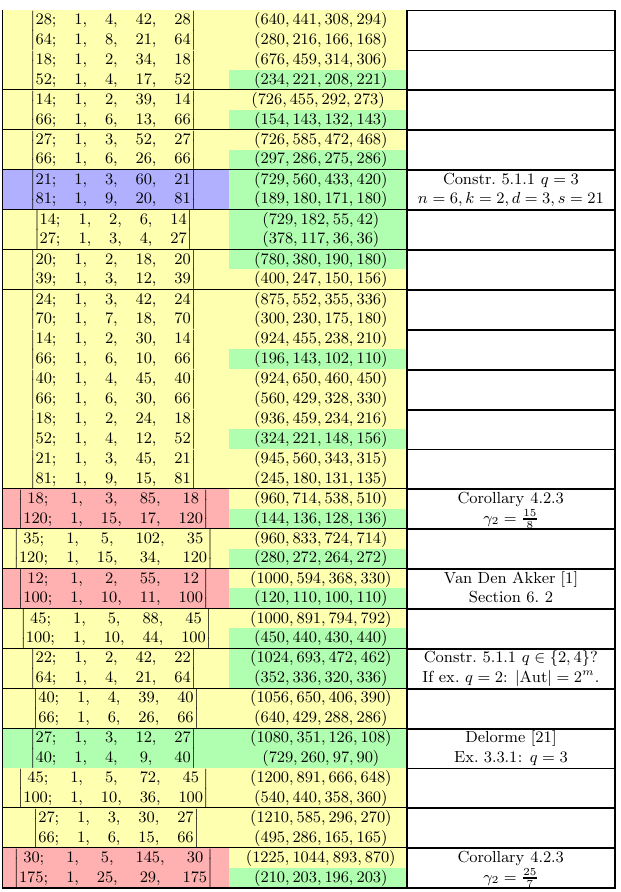
Now back to our work. We describe constructions for which the distance-biregular graph has diameter $ {4}$. Let us look at the table at the end of the preprint, where we list small feasible parameters for DBRGs. Instances of our new constructions are marked in blue:

2.1. Hyperovals

The first blue entry we find is Construction 6.2.2 with the comment “$ {q=2}$”. This is our new infinite family. How does the construction go? We have a geometric and an algebraic explanation. First the geometric one.

1. Fix some $ {q=2^m}$, a point $ {x \in \mathbb{F}_q^3}$, and a projective plane $ {\pi}$ of order $ {q}$ at infinity.
2. Pick a dual hyperoval $ {H^*}$ in the projective plane $ {\pi}$, that is, a set of $ {q+2}$ lines such that every point lies on precisely $ {0}$ (exterior points) or precisely $ {2}$ lines of $ {H^*}$ (interior points).
3. Let $ {Y’}$ be the set of affine planes which meet $ {\pi}$ at infinity in a line of $ {H^*}$ and which do not contain $ {x}$.
4. Let $ {Z’}$ be the set of points $ {y \in \mathbb{F}_q^3}$ such that $ {\langle x, y \rangle}$ meets $ {\pi}$ in an exterior point.
5. Now $ {Y’}$ and $ {Z’}$ form two halves of a DBRG $ {\Gamma’}$ with two vertices adjacent if they are incident.

This very concise and beautiful. The one half corresponds to a strongly regular graph which was first described by Huang, Huang, and Lin in 2007. (A few years ago, Andries Brouwer taught me about it in the context of us writing this paper.) The other half is a complete multipartite graph.

The algebraic explanation is maybe more beautiful for its generality. It is just that we do not know any other examples for which it can be applied (so far at least). In the above, if you forget about $ {x}$ and just consider all points of $ {\mathbb{F}_q^3}$ for $ {Z}$ as well as all points affine planes which meet $ {\pi}$ in a line of $ {H^*}$ for $ {Y}$, then we obtain a DBRG $ {\Gamma}$. The graphs $ {\Gamma}$ and $ {\Gamma’}$ are closely related: Fix a vertex $ {x}$ in $ {Z}$ and look at the induced subgraph of $ {\Gamma}$ for vertices at distance $ {3}$-or-$ {4}$ from $ {x}$. This is $ {\Gamma’}$! We give a general criterion for this which only depends on the parameters of the DBRG.

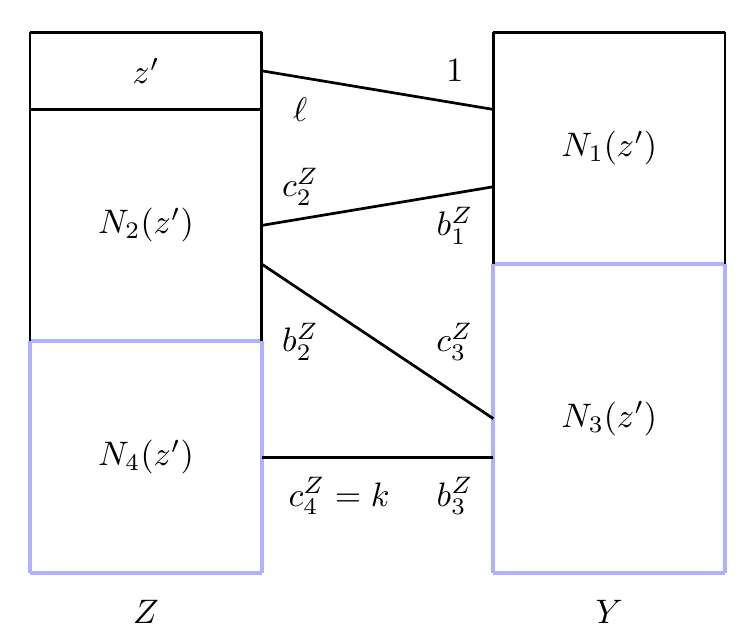
Note that a similar behavior can be observed for strongly regular graphs and distance-regular graphs. Also note that around 10 families of hyperovals are known, I once wrote a table with all of them here!

2.2. Delorme’s Construction, Partial Geometries and Mathon

The second blue entry in our table refers to to Corollary 5.1.1 of our preprint with parameters $ {(n, k, q, d, s) = (6, 2, 3, 3, 21)}$. With so many parameters you might think that this is a new infinite family. Actually, it is not. What do we want? Take a vector space $ {V}$ of dimension $ {n}$ over the field with $ {q}$ elements. Let $ {k}$ be a positive integer with $ {k \leq n/2}$. Then we want a family $ {\mathcal{S}^*}$ of $ {s}$ subspaces of co-dimension $ {k}$ with the following two properties:

1. For all $ {v \in V \setminus \{ 0 \}}$ the number of $ {M \in \mathcal{S}^*}$ with $ {v \in M}$ is either $ {0}$ or $ {d}$.
2. For all distinct $ {M, M^* \in \mathcal{S}^*}$, we have $ {\dim(M \cap M^*) = n-2k}$.

If you have such a set of subspaces, then it gives you many interesting things. We show that it gives you a DBRG. It is also easy to see that it gives you a very special type of two-weight code (which might be interesting for quantum coding theory if I understood and remember a talk by Simeon Ball correctly, but I might misremember). It also gives you a partial geometry.

What are examples for this?

• Hyperovals with $ {(n, k, q, d, s) = (3, 1, 2^m, 2, 2^m+2)}$.
• Maximals arcs with $ {(n, k, q, d, s) = (3, 1, 2^m, 2^{m’}, 2^{m+m’}-2^m+2^{m’})}$.
• The Klein quadric with $ {(n, k, q, d, s) = (6, 3, q, q+1, q^2+q^2+q+1)}$.
• Partial spreads with $ {(n, k, q, d, s) = (2k, k, q, 1, s)}$.
• One construction by Mathon with $ {(n, k, q, d, s) = (6, 2, 3, 3, 21)}$.

Indeed, only the last case is a new distance-biregular graph. All the other examples were already known or are not interesting in this context as they are distance-regular graphs.

3. The Non-Existence of DBRGs & More Comments

Let’s come back to our table. Some entries state are new non-existence results. This is whenever we cite Corollary 4.2.3. Certain numbers depending on the parameters of a DBRG need to be nonnegative integers. If they are not, then we show nonexistence. This actually came up as a side-product of the algebraic explanation of our first new construction using hyperovals.

Then you will notice that sometimes strongly regular graphs for one or both halves are known, while there is no corresponding distance-biregular graph known. We investigated many of these cases. For instance, there is an SRG with parameters $ {(378, 117, 36, 36)}$ which is the complement of $ {NO^+(7, 3)}$. For such small graphs it is easy to check if they extend to a DBRG. If we did this correctly, then it is impossible. As there are many SRGs with such parameters known, we did not add a comment in our table. The situation is different for the SRG with parameters $ {(216, 175, 142, 140)}$. There only one example is known as far as I am aware. And that one does not work.

Lastly, we have a comment for the DBRG with parts of size $ {1024}$ and $ {352}$. This is the smallest open case for the second type of construction which we describe, like Mathon’s. Parameters are $ {(n, k, q, d, s) = (5, 2, 4, 2, 22)}$ or $ {(n, k, q, d, s) = (10, 4, 2, 2, 22)}$. For the first case we tried to assume that symmetry over the field with $ {4}$ elements. Why does it say “If $ {q=2}$” in the table? That is a typo which I noticed while writing this. After lengthy calculations using the computer and Gurobi, we could rule out any automorphisms whose order is not a power of two.

As I have said in the beginning, I am quite excited about these results. Hopefully, our paper will fuel the search for more new distance-biregular graphs.

4. The Twin-Width of “Kind of” and Highly Regular Graphs

My hometown is Darmstadt. Thus, I was excited to learn that with Pascal Schweitzer the TU Darmstadt has a professor who works in areas of combinatorics close to my interests in highly regular graphs. Now whenever I visit my hometown, I can visit his research group and conduct nice research with them. Jointly with Irene Heinrich, a postdoctoral researcher, Simon Raßmann, a PhD student, and Lena Volk, a PhD student, we studied the twin-width of highly regular graphs.

I do not want to write much about that and refer to the paper or Wikipedia for definitions. We determine the twin-width of several relatively simple graphs. We failed at determining the twin-width of slightly more complicated graphs such as all Johnson graphs or generalized quadrangles. One intriguing open question is that of the twin-width of strongly regular graphs. If a strongly regular graph has parameters $ {(v, k, \lambda, \mu)}$, then its twin-width is at least

$$ \min( 2(k-\lambda-1), 2(k-\mu)). $$

All strongly regular graphs which we investigated (all SRGs with up to 36 vertices, some simple infinite families, several millions from my collection) actually have this twin-width. Nonetheless, we are convinced that there must be SRGs for which this bound is false. Maybe some reader here can solve this?

5. A Cover Problem in Teichmüller Spaces

Lastly, I collaborated with Ni An, a PhD student at SUSTech who works in topology, and Ingrid Irmer, a colleague at SUSTech. As I have no understanding of topology, let me translate the problem to language which I understand (based on what my co-authors told me):

We are looking at so-called Teichmüller spaces. These spaces are very complicated. Sometimes you know about a certain behavior in high dimensions, but you would like to have examples in small dimension. This is good for a combinatorialist. We want to have the smallest examples.

Our specific problem is that of finding a so-called “minimal filling subset” of simple closed geodesics of certain hyperbolic surfaces, giving the first low dimensional examples. Do I understand the words, which I just wrote, well? Probably not. But, luckily, it turns out that this is essentially a covering problem with some additional combinatorial constraints. We all know that these are often best solved with a integer linear programming solver like Gurobi (see above). Thus, I could be of help. Here is the tables summarizing our results:

The case for $ {m=7}$ was much work and took us a long time. We used Gurobi together with many possible tricks plus some deeper geometric insights. The methods we use are all standard, I think, but we had to work hard to combine them all, so that we got the computation time down from “only God knows how long” to a few days on modern hardware.

The preprint has many nice pictures: