Constructing Cospectral Graphs

Last week I had a cold and could not do much thinking. So I spent my time making TikZ pictures for an upcoming talk of mine. This talk is on my recent work with Akihiro Munemasa on constructing cospectral strongly regular graphs. I think that the pictures are nice for a blog post, so here we go.

1. The Spectrum of a Graph

Two graphs $ {\Gamma}$ and $ {\overline{\Gamma}}$ are called cospectral if their adjacency matrices $ {A}$ and $ {\overline{A}}$ have the same eigenvalues. This is the same as saying that there is an orthogonal matrix $ {Q}$ with $ {\overline{A} = Q^T A Q}$. Any permutation matrix is a valid choice for $ {Q}$, but this is not very interesting as then $ {\Gamma}$ and $ {\overline{\Gamma}}$ are isomorphic. Chris Godsil and Brendan McKay described one of the easiest interesting choices for $ {Q}$ in 1982. For a graph $ {\Gamma}$ on $ {v}$ vertices, a simplified version of their matrix is

$ \displaystyle Q = \begin{pmatrix} \frac{1}{m} J_{2m} – I_{2m} & 0 \\ 0 & I_{v-2m} \end{pmatrix}. $

Here $ {J_x}$ is the $ {x \times x}$ all-ones matrix and $ {I_x}$ is the $ {x \times x}$ identity matrix. Denote the first $ {2m}$ vertices of $ {\Gamma}$ by $ {C}$ and the remaining vertices by $ {D}$. Then $ {Q^T A Q}$ is again the adjacency matrix of a graph if the following is satisfied:

• The induced subgraph on $ {C}$ is regular.
• Every vertex in $ {D}$ is adjacent to $ {0}$, $ {|C|/2}$ or $ {|C|}$ vertices of $ {C}$.

The new graph $ {\overline{\Gamma}}$ with adjacency matrix $ {\overline{A}}$ can be obtained from $ {\Gamma}$ by modifying the edges of $ {\Gamma}$ as follows:

• If $ {x \in D}$ has $ {|C|/2}$ neighbours in $ {C}$, so $ {|\Gamma(x) \cap C| = |C|/2}$, then $ {\overline{\Gamma}(x) \cap C = C \setminus \Gamma(x)}$.
• Otherwise, do not change the neighborhood of $ {x \in D}$.

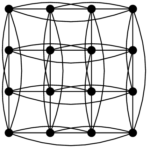
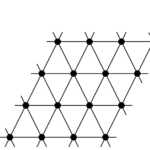
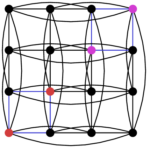
This is known as Godsil-McKay (GM) switching. A nice example for cospectral graphs, which I stole from Andries E. Brouwer’s homepage on strongly regular graphs, are the $ {K_4 \times K_4}$ graph and the Shrikhande graph:

Both graphs have $ {16}$ vertices, each vertex has $ {6}$ neighbors, two adjacent vertices have $ {2}$ neighbors in common as do two non-adjacent vertices. This implies that both graphs are cospectral (their spectrum is $ {6^1 2^6 (-2)^9}$). There many ways to see that these are not the same graphs, for example $ {K_4\times K_4}$ has cliques of size $ {4}$, while the Shrikhande graph does not.

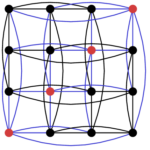
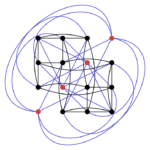
We can identify a set $ {C}$, here in red, and obtain a new graph by applying GM switching:

It is maybe not obvious, but the second graph is again the Shrikhande graph. We can also compare the adjacency matrices, here the adjacency matrix of $ {K_4\times K_4}$:

And here adjacency matrix after switching:

2. A Second Switching

Some time ago, I constructed new strongly regular graph with the same parameters as so-called collinearity graphs of polar spaces. This generalized work by Abiad and Haemers as well as Barwick, Jackson and Penttila, who both used Godsil-McKay switching. My construction was purely geometrical and very specific to the investigated graph. It did not provide a general method for obtaining cospectral graphs. My work with Akihiro Munemasa focused on amending this by finding the matrix $ {Q}$ that belongs to my old switching and finding a general rule similar to Godsil-McKay switching for obtaining cospectral graphs. We succeeded with this last September (in 2018), but it turned out that Wang, Qiu, and Hu already had a paper submitted at that time which described the same switching (which now appeared in Linear Algebra and its Applications). The matrix used this time is

$ \displaystyle Q = \begin{pmatrix} I_{m} – \frac{1}{m} J_{m} & \frac{1}{m} J_m & 0 \\ \frac{1}{m} J_m & I_m – \frac{1}{m} J_m & 0 \\ 0 & 0 & I_{v-2m} \end{pmatrix}. $

A simplified description is as follows. We partition the vertices of $ {\Gamma}$ into $ {C_1 \cup C_2 \cup D}$ such that

• the induced subgraph on $ {C_1}$ is $ {a}$-regular,
• the induced subgraph on $ {C_2}$ is $ {a}$-regular,
• the induced subgraph on $ {C_1 \cup C_2}$ is $ {b}$-regular,
• each vertex $ {x \in D}$ satisfies $ {\Gamma(x) \cap (C_1 \cup C_2) \in \{ C_1, C_2 \}}$ or $ {|\Gamma(x) \cap C_1| = |\Gamma(x) \cap C_2|}$.

The new graph $ {\overline{\Gamma}}$ can be obtained from $ {\Gamma}$ by modifying the edges as follows:

• If $ {x \in D}$ has $ {\Gamma(x) \cap (C_1 \cup C_2) = C_1}$, then $ {\overline{\Gamma}(x) \cap (C_1 \cup C_2) = C_2}$.
• If $ {x \in D}$ has $ {\Gamma(x) \cap (C_1 \cup C_2) = C_2}$, then $ {\overline{\Gamma}(x) \cap (C_1 \cup C_2) = C_1}$.
• Otherwise, do not change the neighborhood of $ {x \in D}$.

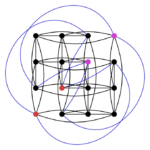
Let’s call this WQH switching. Similar to Godsil-McKay switching, we can apply WQH switching to $ {K_4 \times K_4}$ to obtain the Shrikhande graph. Here $ {C_1}$ is in red and $ {C_2}$ in blue.

This time, we had to change far fewer edges and the second graph looks prettier. For $ {m=2}$ GM switching and WQH switching always yield isomorphic graphs, so we cannot actually obtain new graphs this way. The true usefulness of WQH switching comes for $ {m>2}$. Again, we can provide the adjacency matrices. Here for $ {K_4\times K_4}$ we have still have the following adjacency matrix:

And here for the Shrikhande graph:

WQH seems to become very useful for $ {m > 2}$ in geometric settings. Akihiro Munemasa and I used it to construct strongly regular graphs related to designs as well as polar spaces/orthogonality graphs. I also have nice pictures for that part, but no time to incorporate them into this post. You can read our preprint for more details. There is also much to be said about why people care about constructing new strongly regular graphs or cospectral graphs. The purpose of this post was to put my pictures somewhere and not explaining too much, so I might address this in the future.