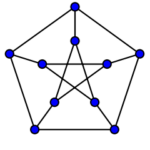
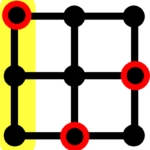
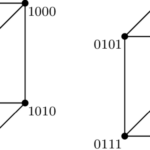
A Very Short History of Pseudorandom Cliquefree Graphs
I started writing this blog post some months ago. Occasion was that my paper “A construction for clique-free pseudorandom graphs” (in joint work Anurag Bishnoi and Valentina Pepe) was accepted by Combinatorica with minor revisions. More precisely, one of the referees was unfavorable of publication because he got the impressions that we are simply restating […]